I. Congruenţa triunghiurilor oarecare 1. Criteriile de congruenţă a triunghiurilor a) L.U.L. = Latură – Unghi – Latură; b) U.L.U. = Unghi – Latură – Unghi; c) L.L.L. = Latură […]

I. Ce este regula de trei simplă Regula de trei simplă este o metodă matematică ce se bazează pe: a) egalitatea produselor pe diagonale; b) calcularea unei necunoscute atunci când se […]

1. Ce este regula de trei compusă Regula de trei compusă este o metodă matematică ce se bazează pe două reguli de trei simple. 2. Când se foloseşte regula de […]

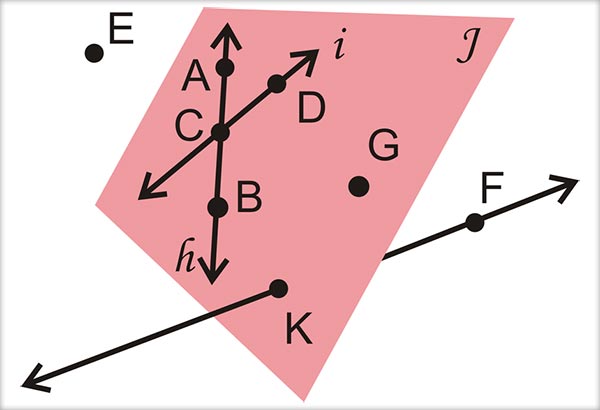
Noţiunile fundamentale ale geometriei sunt: a) punctul; b) dreapta; c) planul. Acestea nu se definesc, ci pot fi descrise. 1. Punctul Punctul poate fi considerat urma vârfului unui creion bine […]

I. Bisectoarele unui triunghi 1. Proprietatea bisectoarei (unui unghi) Un punct din interiorul unui unghi propriu aparţine bisectoarei unghiului dacă şi numai dacă distanţele de la punct la laturile unghiului […]