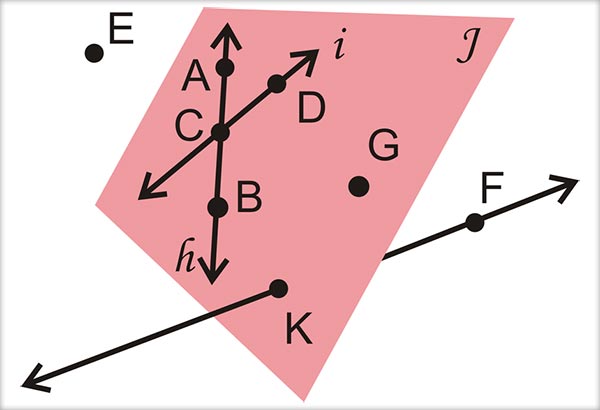
Noţiunile fundamentale ale geometriei sunt:
a) punctul;
b) dreapta;
c) planul.
Acestea nu se definesc, ci pot fi descrise.
1. Punctul
Punctul poate fi considerat urma vârfului unui creion bine ascuţit, lăsată pe foaia de hârtie atunci când o atinge.
Reprezentăm punctul printr-o bulină sau prin două liniuţe care se intersectează.
Un punct se individualizează prin poziţia lui.
Punctele se notează cu litere mari.
O mulţime nevidă de puncte se numeşte figură geometrică.
2. Dreapta
Putem sugera imaginea unei porţiuni dintr-o dreaptă printr-un fir de aţă foarte subţire, bine întins.
Dreapta este o figură geometrică (o mulţime de puncte) şi este nelimitată.
Pentru a reprezenta în desen o dreaptă utilizăm rigla.
Dreapta se notează cu o literă mică sau cu două litere mari, prin care am notat două puncte distincte ce aparţin dreptei.
2.1. Axioma dreptei
Două puncte distincte determină o dreaptă şi numai una.
Orice dreaptă conţine cel puţin două puncte distincte.
2.2. Poziţiile relative ale unui punct faţă de o dreaptă
Faţă de o dreaptă, un punct poate fi interior (aparţine dreptei), respectiv exterior (nu aparţine dreptei).
2.3. Puncte coliniare
Trei (sau mai multe) puncte sunt coliniare, dacă există o dreaptă care să conţină cele trei puncte.
3. Planul
Imaginea unei porţiuni dintr-un plan este sugerată prin suprafaţa apei liniştite dintr-un vas.
Descriem planul ca pe o suprafaţă netedă, întinsă la nesfârşit în toate direcţiile, alcătuită din puncte.
Un plan se notează cu o literă din alfabetul grecesc sau prin trei litere mari puse într-o paranteză rotundă, cu condiţia ca cele trei litere să reprezinte notaţiile a trei puncte necoliniare ce-i aparţin.
3.1. Poziţiile relative ale unui punct faţă de un plan
Faţă de un plan, un punct poate fi interior (aparţine planului), respectiv exterior (nu aparţine planului).
3.2. Dreaptă inclusă în plan
Dacă o dreaptă d are toate punctele într-un plan α, atunci dreapta d este inclusă în planul α.
Punctul, Dreapta, Planul