I. Relaţii metrice în triunghiul dreptunghic
1. Proiecţii ortogonale pe o dreaptă
a) Se numeşte proiecţia ortogonală a unui punct pe o dreaptă:
– piciorul perpendicularei duse din acel punct pe dreaptă.
b) Se numeşte proiecţia ortogonală a unei figuri geometrice pe o dreaptă:
– mulţimea proiecţiilor punctelor acelei figuri pe dreaptă.
1.1. Teoreme
1) Proiecţia unui segment pe o dreaptă este un segment sau un punct.
2) Proiecţia unui segment pe o dreaptă are lungimea cel mult egală cu lungimea segmentului proiectat.
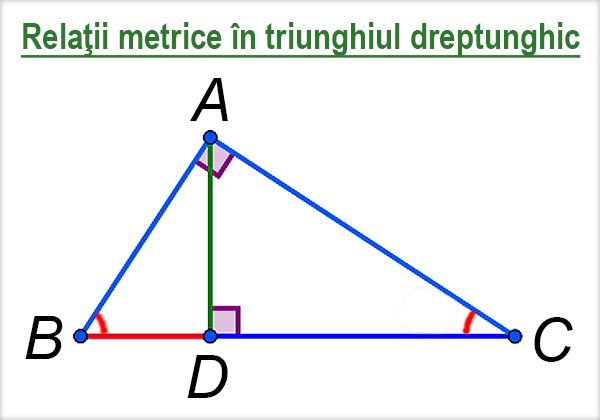
2. Teorema înălţimii
Într-un triunghi dreptunghic pătratul lungimii înălţimii duse din vârful unghiului drept este egală cu produsul lungimii proiecţiilor catetelor pe ipotenuză.
AD2 = BD · DC
3. Teorema catetei
Într-un triunghi dreptunghic, pătratul lungimii unei catete este egal cu produsul dintre lungimea ipotenuzei şi lungimea proiecţiei catetei pe ipotenuză.
AB2 = BC · BD
AC2 = BC · DC
4. Teorema lui Pitagora
Într-un triunghi dreptunghic pătratul lungimii ipotenuzei este egal cu suma pătratelor lungimilor catetelor.
BC2 = AB2 + AC2
5. Reciproca teoremei lui Pitagora
Dacă într-un triunghi pătratul lungimii unei laturi este egal cu suma pătratelor lungimilor celorlalte două laturi atunci triunghiul este dreptunghic.
Dacă BC2 = AB2 + AC2 atunci ΔABC este dreptunghic.
II. Rapoarte constante în triunghiul dreptunghic
sin, cos, tg, ctg
Sinusul, cosinusul, tangenta şi cotangenta se numesc funcţii trigonometrice şi se notează cu sin, cos, tg, respectiv ctg.
1. Sinusul unui unghi
Într-un triunghi dreptunghic considerând măsura unui unghi ascuţit numim:
– sinusul lui, raportul dintre lungimea catetei opuse unghiului şi lungimea ipotenuzei.
sin B = AC/BC
sin C = AB/BC
2. Cosinusul unui unghi
Într-un triunghi dreptunghic considerând măsura unui unghi ascuţit numim:
– cosinusul lui, raportul dintre lungimea catetei alăturate unghiului şi lungimea ipotenuzei.
cos B = AB/BC
cos C = AC/BC
3. Tangenta unui unghi
Într-un triunghi dreptunghic considerând măsura unui unghi ascuţit numim:
– tangenta lui, raportul dintre lungimea catetei opuse unghiului şi lungimea catetei alăturate lui.
tg B = AC/AB
tg C = AB/AC
4. Cotangenta unui unghi
Într-un triunghi dreptunghic considerând măsura unui unghi ascuţit numim:
– cotangenta lui, raportul dintre lungimea catetei alăturate unghiului şi lungimea catetei opuse unghiului.
ctg B = AB/AC
ctg C = AC/AB
5. Reţineţi!
Aria unui triunghi este egală cu jumătate din produsul lungimilor a două laturi şi sinusul unghiului cuprins între ele.